The Christmas tree project that I am working on at the moment uses a series of cones to form the branches. How to join the naturally circular cone to a square section tube? Time to break out the maths!

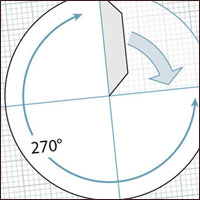
The lowest cone on the tree is make by wrapping round a three quarter circle of paper. A full circle is 360° so 3/4 of a circle is 360 x 0.75 = 270° 

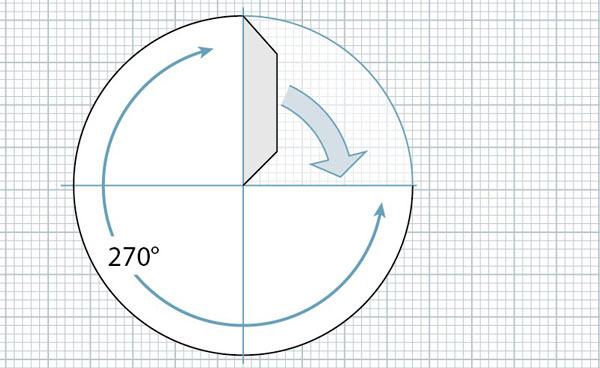
On a flat circle, to cut a square hole in the centre, each side of the hole is rotated 90° compared to the previous side. For three quarters of a circle we'll rotate each side three quarters of ninety degrees.

0.75 x 90° = 65°

And we end up with this open sided shape. (below right)

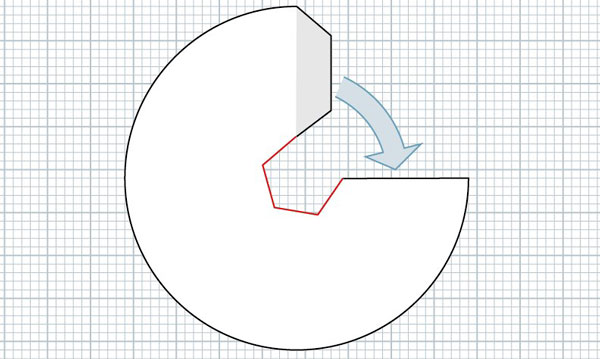
I've fitted the freshly minted shape into the cone – shown in red below. I just need to add some tabs and it will be ready to print out and go.

Works a treat! I scaled the cone up ever so slightly (103%) so that it is a loose fit and glued it into place on the top of the tube. The middle cone has a slightly different angle so the inner shape will need recalculating but the top cone has no hole so that one will be simple!

Maths. It works.