
The dome on the recent Flying Saucer project was a rough representation of half a sphere. I could have used Blender to create the net as I did in the banana but decided to use maths. Sometimes its quicker to walk than take the bus.
The original design was based on a dome with a radius of 50mm. I decided to divide it into seven sections round by three sections high. You could change this number if you wanted by changing the numbers in the equations that follow.
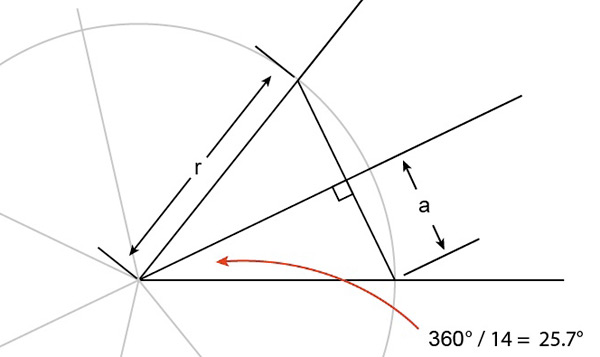
To find the length of each side I've used a bit of basic geometry. For this I divide each section into two to make two right angled triangles. I know the length of the long side (the hypotenuse, r) and the angle in the corner so I can find out the length of side a, then double it to find out the length of each side of the seven sided shape.
The corner angle is 25.7° (360/14) To calculate the length 'a' multiply the length of the long side 'r' by the sine of the corner angle. Google is your friend here. You can find out the value simply by entering "sin 25.7 degrees" as a search. Make sure you use the word 'degrees' in your search otherwise it will give you the answer in radians as I found out. Eventually.
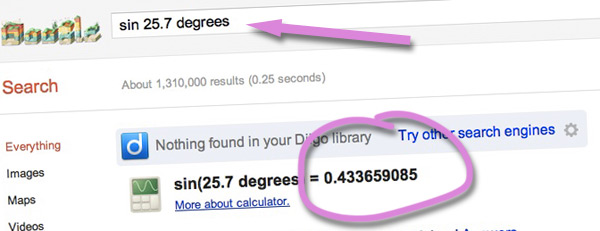
Multiply the answer by 50 to find out the length 'a'. You can use Google again can help you with your calculation. Simply type 50*0.433 into the search box. (The asterisk sign is used as the multiplication sign in computer programming, and web searches) Double it to find the length of each side. It turns out is is 43.3mm. Okay – one down, what's next.
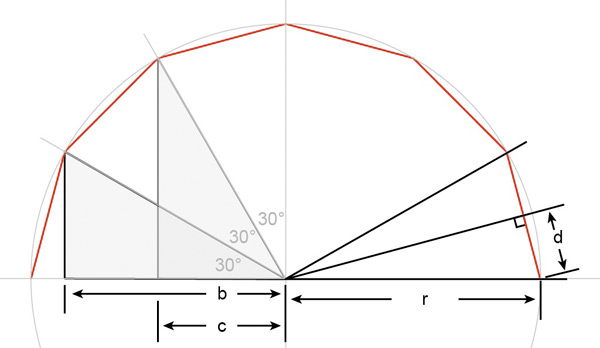
This is a side view of the dome. Each of the three horizontal strips is 30° wide. To work out how high each strip is ('d' x 2) we can use the same technique as with the previous example but this time using sine of 15°. Google says it is 0.259 with a bit of rounding. Double it and multiply by 50 to get a strip with of close enough to 26mm.
Finally, the values of 'b' and 'c' show how much the side tapers. We don't need an actual length, just a ratio compared to the radius. This time the angles we know are adjacent to the length we are looking for so we'll use cosines. b = cos 30° and c = cos 60°. Back to Google
b= 0.8660 (that's one I always remember!)
c= 0.5 (I remember that too 🙂
So the final step…
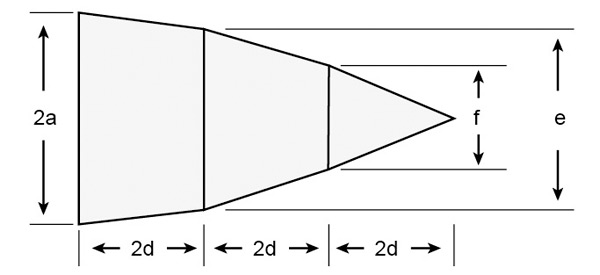
This is the shape of each segment plotted onto a computer. We calculated the width 2a (43mm) first then the length 2d which turned out to be 26mm. Starting with the four sided shape on the left, the left hand edge is 43mm, the right hand edge of that shape needs to he tapered down to the length 'e'. Multiply 43mm by 0.8660 (remember?) resulting in a length for 'e' of approx 37mm.
The final length is 'f' This is 43mm multiplied by 0.5, the value of 'c', which is 21.5mm.
Plot it all out as above to make one segment.
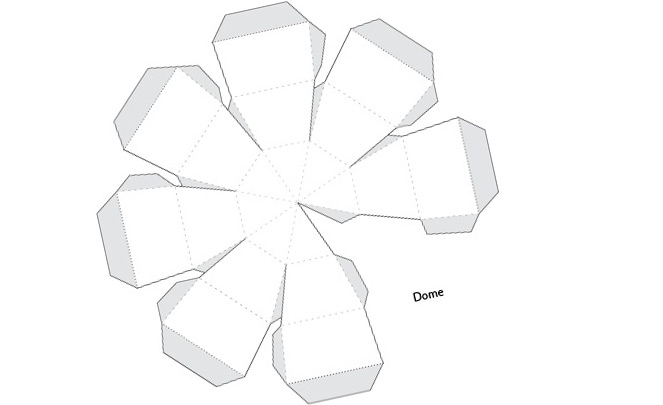
Copy seven segments, rotating each one by 45° and join 'em up!
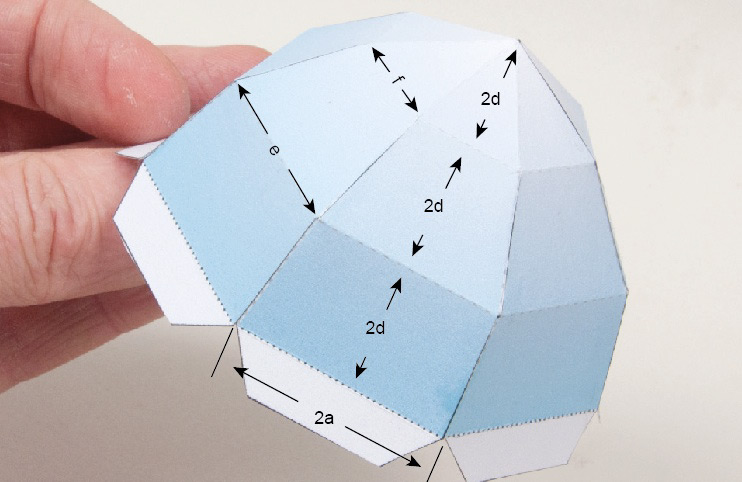
And there it is.
To make the seven sided hole in the saucer section I used the same technique I'd used on the Christmas Tree here.
Glue it all together.
"You have the Bridge Mr Worf."


