Paper is intrinsically flat. Not suited for making spheres. To make curves takes geometry. There are a few ways of approximating a sphere from paper including making multi-faceted shapes or, as in this case, slicing up the surface and rebuilding it in strips.

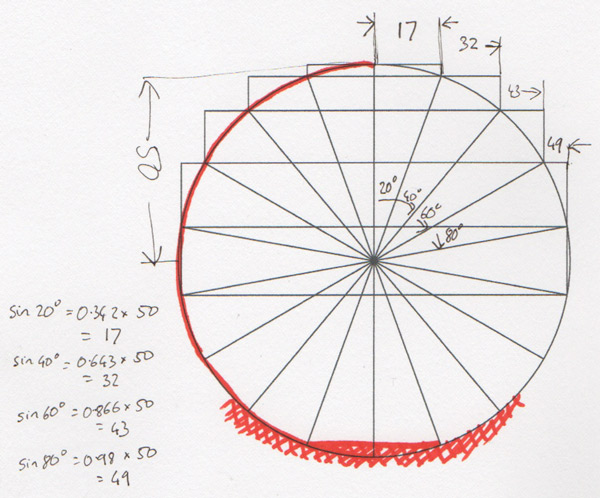I’ve decided to split the sphere into twenty degree slices from top to bottom. Vertically I’m using ten strips.

Each horizontal slice is effectively a circle. I can work out the radius of each of the circles using the sine of the angle. For example, the top slice is twenty degrees down, sin 20 ° is 0.342, multiplied by the radius of the sphere, 50mm, gives a radius for that slice of 17mm

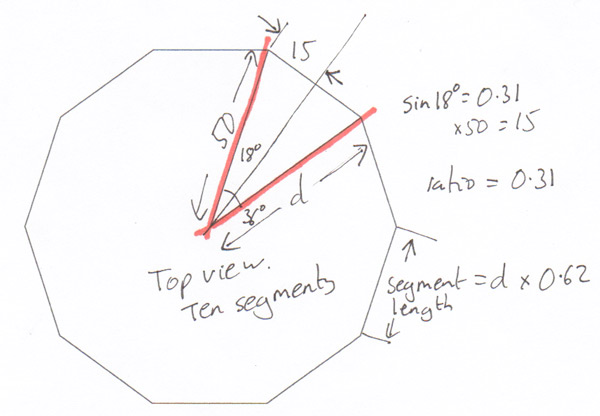Looking down from the top to see the ten segments making up the sphere. With a bit more geometry I’ve worked out the multiplier to calculate the segment width at each slice. Turns out it is 0.62.

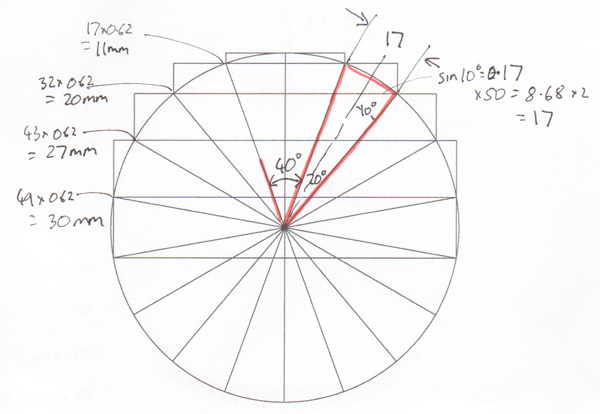So for example at the 40 ° level the radius of the slice is 32mm. Multiply that by 0.62 to get a slice width of 20mm. Yay maths!

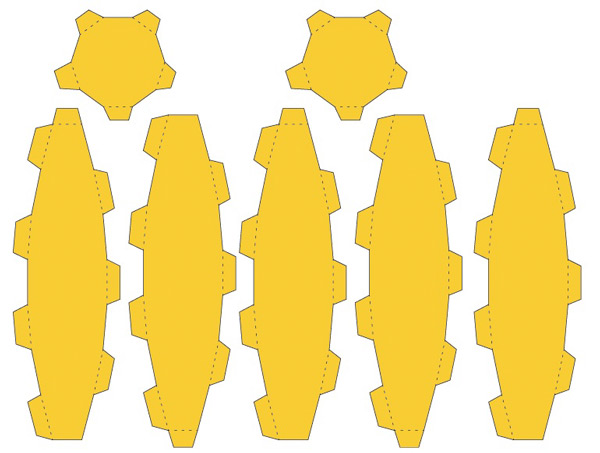
Having worked out the widths of the segment at each level it is simply a case of transfering the numbers to Illustator, creating a slice then making nine more copies. The addition of a top and bottom disk completes the parts

Once everything is printed out, I cut the bits out and started gluing them together.The downside of side a fine grained globe model like this is that there are a lot of tabs to glue, ninety if my maths hasn’t let me down.

Still, I think it is worth the effort.