I've finished sizing up the Toroid model today as well as getting the new look web site ready for roll out. Busy day!

The toroid model had loads of fun maths in it which I've gone over below. Enjoy.

Okay – so I'm breaking the fourth wall but really, how are you supposed to take pictures with your left hand?

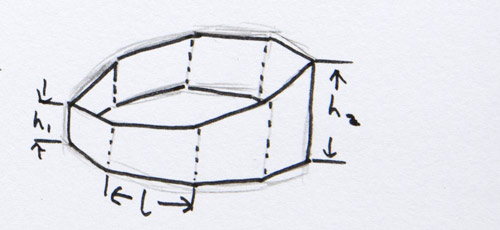
I've divided the donut into 11 wedges, each made from an eight sided shape. I know that the angle of each section is approx 32.7 degrees. (360/11) To create each piece I need to work out the minimum height (h1), the maximum height(h2) and the length of each of the faces (L)

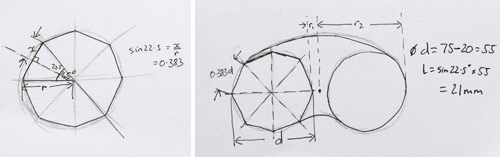
Okay – L first.

I'm aiming at a donut with inner radius of 20mm and an outer radius of 75mm. That means that the actual donut body (d) has a diameter of 55mm (75mm-20mm) Using trig above that means that the length of each face is close enough to 21mm as makes no difference. (sin 22.5 x 55mm)

So that's L sorted.

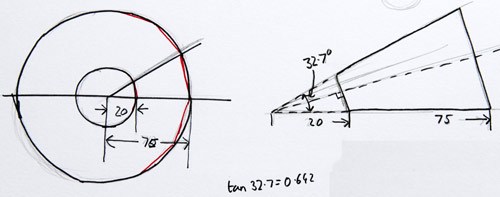
For the two heights I'll switch to a plan view of the donut. I've already established that the angle is 32.7 degrees. I'll use tan this time because I'm looking for the hypotenuse. So,  tan 32.7 is 0.642. To work out the two heights I just need to multiply the two radii by this figure giving: h1 = 13mm and h2 = 48mm.

So there you have it – donuts by numbers – and that's why I love maths.

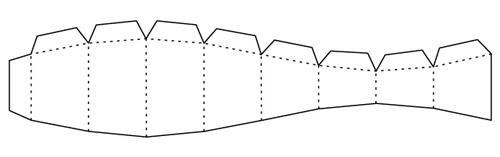
Now I just need to print out eleven of these and hope that they stick together correctly.

That'll have to wait – friends visiting.