I received the by now traditional Simpson socks for Father's day and as you would imagine, this got me thinking about doughnuts. A quick search on google turned up nothing by way of toroid nets. Time to get the brain into gear. I had a vague memory of a toroid shape made up of sections in an advert for Mathematica, but how to design the section?
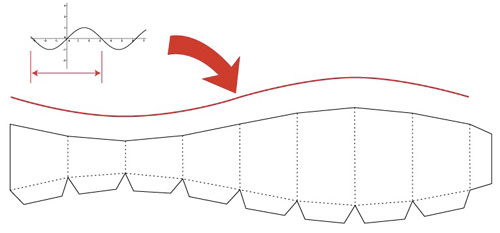
Each section is a kind of circular wedge. The net for that would have a sine wave edge. So, create sine wave, sample 360 degree section of same, stretch to appropriate size.
I then flipped over a copy, added evenly spaced vertical sections (8 of them) and created the net for a single section complete with tabs that you see above.

It worked surprisingly well! Notice that even though the edge is based on a curve it sits nice and flat on the work surface. Lovely.
There is a certain amount of guess work involved here. How steep should the angle of the wedge be? How many sections will I need? These two numbers are connected but I'm not sure how. Time to cut out and try.

I glued six sections together and created this shape which looks like it is just short of half a doughnut.

Too save time and cutting, here is the same shape held up to a mirror. Two more sections I reckon, making fourteen in total. I'm really not sure how I'm going to glue the last piece into place!
Fourteen seemed like a lot of parts so I tried the same again but with much thicker wedges. The result is in the square photo at the top. Looks like seven wedges for a complete shape . Looking at it, though, I think the fourteen wedges are worth the extra effort.
Colour and sprinkles next!
——–
I've added the file with the parts as they are so far if you want a try. Member's download below.


